Supervisors: K.-R. Müller, W.-C. Müller, F. Noé

Doctoral researcher: Saeed Salehinajafabadi

Background: The numerical cost of turbulence simulations and the lack of a comprehensive theory motivates the search for reduced-order models of this phenomenon. A preceding project on a scalar network model of turbulence dynamics has shown that the nonlinear energy dynamics of turbulent flows is well captured in a reduced Fourier representation. The model abstracts turbulence as an ensemble of discrete, nonlinearly interacting agents exchanging energy.

Objective: A possible way to diminish the model’s level of abstraction is the incorporation of spatial flow structure obtained via Machine Learning methods applied to flow simulation data.
To this end, this spatial information has to be associated with the above-mentioned agents. This will offer the opportunity to include the lacking spatial phase information in the reduced scalar representation of the flow. The approach can, as a side-effect, also generate physical insight on turbulence on a fundamental level.

Supervisors: C. Schuette, F. Noé, M. Weber

Background: The problem of determining the rate of rare events in dynamical systems, e.g., rate for molecular conformation changes or on- and off-rates in drug design, is quite well-known but still difficult to solve. Most of the attempts to overcome this problem can be linked to finding almost invariant subspaces of so-called transfer operators. There are several novel data-based approaches that utilize kernel learning and deep learning approaches. The essential question is how to learn dominant subspaces from sparse data on the fly with sufficient accuracy.

Objective: For very large systems, dimension reduction of the problem seems necessary. The identification of meaningful low-dimensional representations of the dynamical behavior, e.g. via reaction coordinates, plays a key role in the study of complex molecular systems. Recently, precise defining characteristics of such reaction coordinates were identified and linked to the existence of a so-called low-dimensional transition manifold. One essentially open problem is the combination of the rare event sampling techniques with the novel transfer-operator-based approaches targeting reaction coordinates (characterize the transition manifold locally, on the fly, and continue along its tangential directions). The objective of the project is to solve this problem.

Main Supervisor: G. Steidl
Additional Supervisors: F. Noé, C. Schütte

Doctoral Researcher: Florian Beier

Background: The classical problem of optimal transport (OT) dates back to the work of the French mathematician Monge in the 18th century and was brought into the relaxed form which is mainly considered today by the Soviet mathematician Kantorovich in the 1940s. Over the years, the problem has been greatly generalized in particular by the work of Villani and is nowadays a popular choice for tackling various problems in imaging sciences, computer graphics and machine learning. Steidl’s group is working on dynamical imaging for a long time. OT is just one approach that nicely joins methods from optimization theory, convex analysis, PDEs and measure theory.

Objective: In this project, we will investigate unbalanced multi-marginal regularized OT and combine it with coherent set detection from a whole time series of densities given by particles which cannot be tracked individually. Additionally, we want to understand the OT of measures having a certain number of vanishing moments as well as OT on special manifolds. Efficient algorithms for tree-structured costs, in particular for the computation of multiple barycenters will be developed.

Supervisor: F. Noé
Additional supervisors: K.-R. Müller, J. Hermann

Doctoral Researcher: Atharvar Kelkar

Background: Machine-learning (ML) approaches to compute and simulate molecular interactions have become very powerful and popular in the past few years and are poised to help designing molecules and materials with novel properties in silico. An outstanding example are neural networks for learning quantum chemical energies. These networks have been shown to reach the accuracy of the quantum Chemistry methods used to compute the training data, but they have an important limitation which currently prevents their use for the simulation of large-scale molecular systems: they are short-ranged. Short-ranged means they only compute direct particle- particle interactions and typically do that using a cut-off, i.e. they only compute nearest neighbor interactions. However, electrostatic interactions are fundamentally long-ranged, meaning that they cannot be cut off without making errors that have the same magnitude as the total interaction energy.

Objective: In this project we want to develop the next generation of neural networks for computing molecular interactions that explicitly incorporate the capability to represent long-range interactions, and we will employ these networks in the development of efficient force fields for the simulations of materials, which are important for the design of new solar cells, catalysts and many other applications.

Main Supervisor: C. Clementi
Additional Supervisors: K.-R. Müller, F. Noé

Doctoral Researcher: Nicholas Charron

Details will follow soon.

Supervisor: W.-C. Müller
Additional supervisors: A. Ghani, J. Reiß

Doctoral Researcher: Lukas Moczarski

Background: Spatio-temporally coherent regions, in particular their boundaries, are often the dynamically most interesting and important parts of fluid-dynamic phenomena. The gradients that typically define these boundaries provide the free energy for propagating or unstable processes driving a system towards energetic equilibrium, e.g. Kelvin-Helmholtz/Rayleigh-Taylor instabilities in turbulence or
concentration/reaction fronts in chemically driven flows.

Objective: This present project focuses on the properties of the regions that drive the boundary dynamics. In the present project, a coherence detection scheme is combined with a physical model of turbulent transport and Lagrangian dynamics to obtain diagnostic information about the interaction of coherent parts of the flow and their nonlinear effects on their incoherent complement and vice versa. We thus aim at building a data-driven self-adjusting flow diagnostic that preferentially examines the dynamics in the most important region for many real-world applications — the boundaries of structurally coherent regions.

Main Supervisor: B. Blankertz
Additional Supervisor: R. Schneider, V. John

Doctoral Researcher: Gabriel Wagner vom Berg

Background: Real-time analysis of brain signals as well as basic and clinical neuroscience can profit from accurate head models. Such physical models of the head and its internal structure establish the connection between the active brain structures and the sensors located on the scalp. Currently, internal parameters like skull thickness and the distribution of the cerebrospinal fluid (CSF) cannot be adequately estimated without resorting to expensive imaging techniques such as magnetic resonance imaging (MRI).

Objective: This project will complement the classic modelling approach of differential equations by data-driven techniques in order to establish a practical and affordable way to estimate accurate individual head models. To that end, a novel application of shape optimization is to be developed to tackle the ill-conditioning of the shape Jacobian. The parametric representation of the head model is challenging due to the complex underlying structure of head tissue surfaces. That will be approached by a novel low-dimensional representation of individual head geometries based on nonlinear methods. Large data bases for the optimization of the representation are available. Validation will be performed on data from a artificial head that is built using 3D printing and EEG that will be recorded within this project.

Supervisors: T. Breiten, J. Reiss, V. John, A. Ghani

Doctoral Researcher: Shubhaditya Burela

Sharp, moving fronts like shock waves or flames cannot be handled efficiently by classical model order reduction methods (MOR), preventing the application of MOR to these costly problems. To overcome this, a substantial methodological progress is necessary. In the previous project a non-linear extensions of classical MOR was found, which can overcome some of the structural problems, namely it can handel transport of sharp fronts with topology changes.

A further, material extension is needed to treat real configuration, consisting of multiple moving fronts and continuous fields. The project aims at the construction of such a method and the application to configurations from combustion physics. The project consists of developing a method to identify low dimensional, non-linear descriptions from relevant large data, construct time dynamic models for
these special descriptions and deploy it finally to reactive flow simulations. By this it combines challenging methodological work with an application in the field of engineering.

Supervisors: V. Mehrmann, A. Ghani, T. Breiten

Doctoral Researcher: Vikas Yadav

Background: Experiments and numerical simulations represent the main pillars in combustion sciences. However, reduced-order models (ROMs) gain popularity since they (i) accurately capture the essential physics, but at the same time, (ii) are computationally fast and facilitate parametric studies. In the context of combustion instabilities, ROMs are widely used, but require very accurate empirical models feed by experiments or numerical simulations.

Objective: In this project, we aim to develop, implement and validate a data assimilation framework, which combines sparse data sets together with a qualitative model to predict the onset of combustion instabilities. First, we apply this framework to a laminar flame and, in a second step, extend to turbulent, swirling flames. To speed up the computation process, we will employ surrogate modeling techniques, such as Gaussian Process and Active Subspace modeling.

Supervisor: W.-C. Müller
Additional supervisor: V. Mehrmann

Doctoral Researcher: Maria Mathew

Background: In a previous project, we have developed a reduced scalar model of turbulent energy dynamics in magnetohydrodynamic (MHD) flows which is based on interacting groups of Fourier space ‘modes’.
The model is able to reproduce turbulent nonlinear interactions of fluctuations of comparable spatial extent (local interactions). However, some important real-world turbulent systems, e.g. Earth’s atmosphere, exhibit pronounced interactions of structures on disparate spatial scales (nonlocal interactions).

Objective: Thus, there is the need to control the model’s level of locality in order to obtain a better approximation of realistic turbulence. The Fourier ansatz underlying the model can be enhanced accordingly by associating recurring spatio-temporal structures in the turbulent fields with specific excitation patterns in Fourier space. In collaboration with project Q2 that deals with the detection of such structures by machine-learning techniques the present project will explore ways to incorporate this information in the networking framework.

Supervisors: J. Eisert, C. Schütte

Doctoral Researcher: Jonas Fuksa

Much of traditional model building of physical systems is based on basic principles and reasoning about plausible interactions about constituents. Such an approach, however, may be less feasible when many degrees of freedom come into play in an unknown fashion. This applies to problems in biology and chemistry, but also to interacting quantum problems. In recent years, it has increasingly become clear that a data driven approach can fruitfully complement purely differential equation-based modelling. On some occasions, when many degrees of freedom come into play, for a-priory modelling to be feasible, specifically in the biological context, or in applications of the quantum technologies, where dynamical laws must be known to very stringent requirements in precision, a largely data-driven recovery can in instances be the only way forward when aiming at identifying the underlying governing dynamical laws. Given this state of affairs it is no surprise that ideas of data-driven recovery are increasingly moving into the centre of attention.

This project sets out to provide a framework of data-driven recovery of dynamical laws, both in the classical and the quantum realm. In both readings, tensor networks will feature strongly, to overcome the curse of dimensionality. For classical equations of motion, questions of expressivity will feature strongly. In the quantum realm, it is ideas of tensor network recovery, of machine learning and randomized methods such as randomized benchmarking that will take center stage.

Main Supervisors: B. Zwicknagl
Additional Supervisor: G. Steidl

Doctoral Researcher: Anastasija Pesic

Background: Biological membranes are thin structures that are composed of various components. The different components often form microdomains that are arranged in complex
patterns. Several modeling approaches attribute many biological processes to these domains. To explain this pattern formation, variational models have been introduced that couple the local
composition of the membrane to its local curvature. Due to their nonlocal and nonconvex structure, the resulting variational problems are analytically and numerically challenging.

Objective: To explain the formation of different structures, we plan to determine the optimal scaling of the minimal energy in terms of the problem parameters. The more quantitative focus will
lie on the regime in which complex patterns are expected. We plan to combine analytical tools from the calculus of variations with numerical techniques from machine learning and reduced
basis methods to gain better understanding of the experimentally observed patterns.

Main Supervisor: K.-R. Müller
Additional Supervisor:  C. Schütte
Doctoral researcher: Ingo Gühring

Background: The area of data science provides various approaches to identifying structures in high-dimensional data. In numerical analysis of partial differential equations multiscale systems are today a common tool and often guarantee efficient algorithms by providing a decomposition into different resolution levels. Thus, it seems very natural to analyze high-dimensional data with respect to such multiscale structures as well. However, to date almost no approaches exist, and even the question of a precise definition of multiscale structures is far from being solved.

Objective: This project aims to develop a fundamental theory for multiscale structures in high-dimensional data and associated algorithmic approaches for detecting such structures. To achieve this goal, a carefully designed list of mathematical desiderata for multiscale structures will be specified, based on which learning algorithms will be developed and analyzed.

Main Supervisor: K.-R. Müller
Additional Supervisors: W.-C. Müller and F. Noé
Doctoral researcher: Ann-Kathrin Dombrowski

Background: The numerical cost of turbulence simulations and the lack of a comprehensive theory motivate the search for reduced models of this phenomenon. This project will explore the applicability of Machine Learning (ML) techniques to ultra-fast prediction and analysis of turbulence obtained from direct numerical simulations. This radically new approach treats a complex nonlinear differential equation (recently successful for the Schrödinger’s (SE) equation) as a stochastic system and learns from data generated by it. Turbulent systems, e.g., Navier-Stokes and magnetohydrodynamic flow, exhibit due to their nonlinearity a complexity that is at least similar to the SE.

Objective: This project aims to transfer and adapt ML methods for studying multiscale properties of turbulent flow. In addition, the potential of the predictive approach to serve as a new kind of subgrid modeling technique will be investigated. Further study will focus on the usage of ML analysis for tracking structural turbulent flow properties.

Main Supervisor: 
Additional Supervisors: J. Eisert, F. Noé, and C. Schütte
Doctoral researcher: Qiao Luo

Background: In the past years, the classical sparsity model has been extensively explored and utilized. However, depending on the application, the sparsity of data typically exhibits certain structures, giving lately rise to different structured sparsity models. Despite models such as block, fusion frame, and model-based sparsity, research is still in its infancy. In fact, real-world applications require sparsity models with a much more sophisticated inner structure such as multiscale structures with dependencies.

Objective: The objective of this project is to first introduce a suitable model situation for such sparsity structures based on which a flexible theoretical framework including associated dictionary learning algorithms should be developed. This framework shall then be applied to derive model reduction strategies in molecular dynamics where one has to face an entire cascade of temporal and spatial scales bridging many orders of magnitude.

Main Supervisor: F. Noé
Additional Supervisor: K.-R. Müller
Doctoral researcher: Jonas Köhler

Background: High-throughput molecular dynamics (MD) simulations can now sample complex biologically relevant processes such as protein-protein binding. Due to the extensive amount and high dimension of such datasets, the task of analyzing such data and extracting the essential kinetic and thermodynamic features has become a major challenge. The currently most successful techniques to achieve this include Markov state models and blind source separation methods, as they both exploit the essential spectral properties of the Markov operator underlying the MD time series. However, these methods are shallow learning structures and are thus subject to the definition of suitable features, basis functions or kernels, which often leads to unsatisfactory and difficult-to-interpret results in complex MD processes that are often of intrinsically hierarchical nature.

Objective: In this project, we aim to design efficient deep learning structures that learn optimal, nonlinear feature transformations, provide interpretable models of the molecular kinetics, and permit simulating long-time molecular dynamics.

Main Supervisor: B. Blankertz
Additional Supervisors: A. Carpentier and H. Siebert
Doctoral researcher: Oleksandr Zlatov

Background: Brain-Computer Interfaces (BCIs) mostly target medical applications. More recently, BCI research aims at improving human-computer interaction (HCI) in general. For example, in information seeking, users quickly scan through a larger amount of information and provide an explicit response only for few items, while the BCI may concurrently collect and integrate implicit information about all scanned items. Still, a major hurdle in such cases is the relatively long procedure that is required to calibrate the system.

Objective: Recent developments of machine learning in general, and sequential/active learning in particular, are excellent tools to accelerate the calibration in a co-adaptive process between the user and the BCI. Applying those techniques in the context of EEG data with its inherent complexity (spatial/temporal dependency, high dimensionality, etc.) poses considerable challenges that will be tackled in this project.

Main Supervisor: B. Blankertz
Additional Supervisors: A. Carpentier
Doctoral researcher: Nils Harmening

Background: Localization of brain activity is of great importance for clinical applications and for basic neuroscience. However, this is difficult to achieve from surface EEG data as it requires the solution of an ill-posed inverse problem. The most accurate way of (noninvasive) localization is the estimation of individual head models from anatomical MRI scans, which are very costly and time consuming to acquire.

Objective: This project will provide a method to estimate a 4-shell model with the boundary-element-method (BEM) which describes the anatomical and electrical properties of the head of an individual test person. Our proposed methods will use as input data from electrical impedance tomography (EIT) to avoid costly MRI scans. In order to fit the 4-shell BEM to the EIT data, we will exploit a large scale database and develop as well as evaluate different methods to restrict the fitting to a low dimensional search space, based on non-negative matrix factorization and on tensor approximations.

Main Supervisor: C. Schütte
Additional Supervisors: K.-R. Müller and J. Eisert
Doctoral researcher: 

Background: Modeling cellular dynamics is a very active field of research with a huge variety of possible models. Selecting the appropriate model for a certain system is a challenging art, in particular, if a mixture of deterministic and stochastic effects have to be considered. Simultaneously the amount of data that is produced by advanced experimental techniques like single cell analysis is growing exponentially which raises the challenges of identifying appropriate models algorithmically. Recently, new algorithms for finding appropriate differential equation (DE) models based on time-resolved experimental data have been proposed and developed into a family of methods under the name data-driven sparse identification of nonlinear dynamics (SINDy). Presently these algorithms cannot account for the multiscale structure with deterministic and stochastic reactions exhibited by real-life cellular dynamics, and also require the data to be given in time slices with rather small lag times with it almost never valid for real-world data.

Objective: This project aims to develop a new SINDy framework that allows for application to data-based identification of deterministic-stochastic hybrid models.

Main Supervisor: 
Additional Supervisors: 
Doctoral researcher: 

Background: In the context of modeling and quantifying the uncertainty in porous flow models, extremely high dimensional regression problems appear. A very promising novel approach is to cast such problems in a tensor regression framework, which is far from being fully understood. Beyond classical estimation, an almost unexplored question in this context despite its importance for applications is uncertainty quantification.

Objective: This project aims to perform complete inference in the regression model, i.e., not only estimating the parameter in the model but also estimating the precision of the estimators from data. We highlight that the possibility of optimally estimating the solution or the model by minimizing a constrained/penalised risk functional does not imply the possibility of quantifying optimally the risk of the estimator. Our approach will be based on acceleration phenomena for risk estimation combined with machine learning methods, which we expect to also ensure extremely fast and efficient methods in practice.

Main Supervisor: J. Sesterhenn
Additional Supervisor: F. Noé
Doctoral researcher: Paul Schwarz

Background: Fluid dynamic experiments usually suffer from measurement noise and influences of the measurement technique on the flow field, e.g., by probes. Furthermore, there are strong restrictions on measurable quantities, as in general only a subset of quantities is experimentally accessible. However, image-based data assimilation techniques using data from optical methods like PIV or Schlieren enable a reliable analysis of experimental flow configurations by means of image-based data assimilation.

Objective: The main objective of this project is to develop a theoretical foundation for image-based data assimilation, also taking into account compressed sensing ideas on the optimal measurement data to make quantities of interest measurable with minimal effort. Preliminary works on the topic, in particular, the adjoint-based pressure determination from PIV data, already give evidence of the extensive possibilities of image-based data assimilation techniques for research and industrial use.

Main Supervisor: W.-C. Müller
Additional Supervisors: V. Mehrmann, J. Reiss, and R. Schneider
Doctoral researcher: Jiahan Wang

Background: Temporal or spatial structures are readily extracted from complex data by, e.g., modal decompositions like proper orthogonal decomposition (POD) and dynamic mode decomposition (DMD) or Lagrangian coherent structure (LCS) analysis of Lyapunov exponent manifolds. Subspaces obtained by these techniques can serve as reduced order models and define spatial structures in time or temporal structures in space.

Objective: This project aims at combining the mode decomposition and the LCS approach, in particular the underlying statistical sampling of passive tracers, to increase the efficiency of complexity reduction and the robustness of detection of spatio-temporally coherent structures in turbulent flows. We will combine sub-ensembles of tracers associated with an LCS with the mode decomposition representations, since the geometry of these tracer groups should be amenable to complexity reduction by representation of topologically simpler geometrical objects such as ellipsoids or tetrahedra.

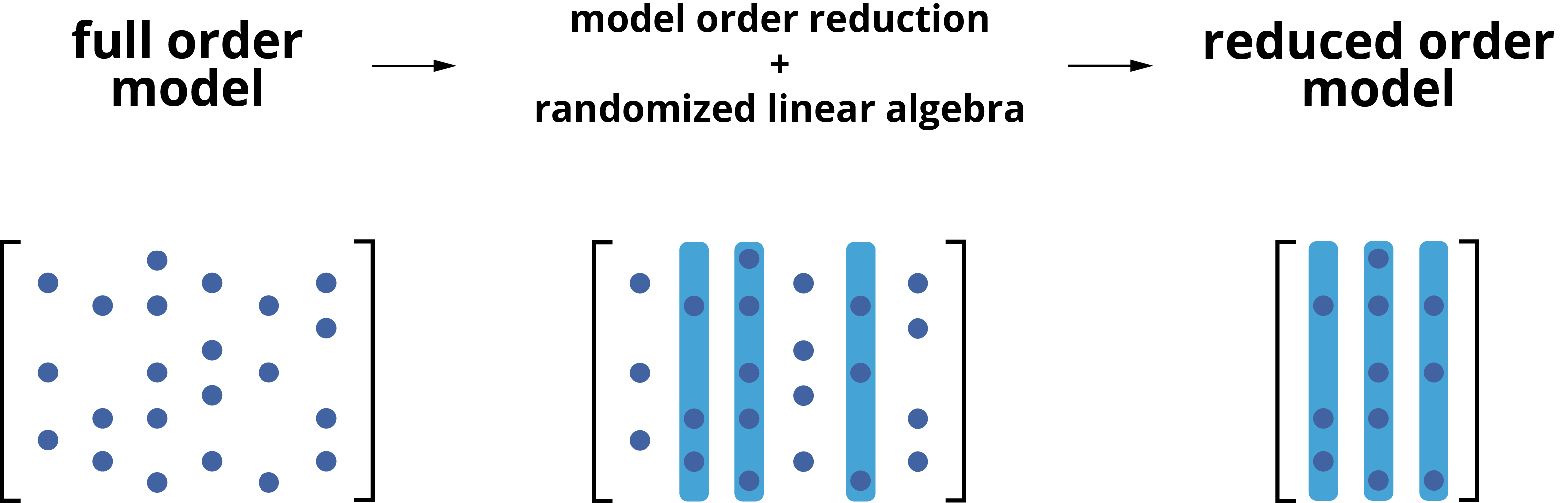
Main Supervisor: V. Mehrmann
Additional Supervisor: M. Voigt
Doctoral researcher: Ines Ahrens

Background: In simulation, control, and optimization for large scale complex systems, model reduction is an essential requirement. Typically model reduction techniques used for the solution of PDEs or control problems are based on SVD-techniques in suitable finite dimensional representation systems. Although this is very successful in many applications, sparsity of the solution or the solution operator is not promoted well.

Objective: The objective of this project is to combine the construction of appropriate representation systems with randomized techniques for the construction of reduced order models and sparse solutions. To achieve this goal, we will exploit adequate multi-level representations of operators and solutions that promote sparsity and combine them with randomized techniques to compute these sparse representations. As model class we will discuss transport equations in reactive flows.

Main Supervisor: W.-C. Müller
Additional Supervisor: V. Mehrmann
Doctoral researcher: Benjamin Beck

Background: The nonlinear dynamics of turbulence represents a longstanding physical and mathematical problem. Incompressible turbulence can serve as a simplified model, since it corresponds to an ensemble of discrete Fourier mode excitations in wavenumber space. The presence of a magnetic field reduces each nonlinear three-mode interaction to a pair exchange mediated by the third mode. Thus, the mathematically difficult quadratic advection nonlinearity becomes amenable to a detailed study in the case of incompressible magnetohydrodynamics (MHD).

Objective: We aim at a detailed understanding of the spectral turbulent transport of ideal invariants such as energy or magnetic helicity in numerical simulations of incompressible MHD turbulence and the development of reduced turbulence models that go beyond the classical shell-model ansatz. Insights gained from the above-mentioned nonlinear dynamics will help to construct a new reduced triad-interaction model of turbulence.

Main Supervisor: V. Mehrmann
Additional Supervisors: J. Reiss and J. Sesterhenn
Doctoral researcher: Philipp Krah

Background: Flows with shocks appear in many technical situations, since a pressure-drop by a factor of two is sufficient to create supersonic flows and thereby nearly inevitable shocks. These shocks are crucial for the performance yet depend sensitively and non-linearly on parameters. Classical methods of model reduction in industrial use, like the POD often fail at the very positions of the shocks.

Objective: The goal of this PhD project is to study the new shifted POD method for shocks in transonic flows, and to produce parameterized reduced order models. This new method offers a way to circumvent structural problems and allows an efficient optimization of a configuration. Optimal configurations predicted in the low dimensional model will be validated via simulation and then be improved by expansion of the model. This would lead to an important methodological progress in this field, which will be tested in the reduction of total pressure loss in the optimization of internal flows.

Main Supervisor: R. Schneider
Additional Supervisor: W.-C. Müller
Doctoral researcher: Leon Sallandt

Background: The minimizer of an optimal control problem for a Bolza type functional constrained by a system of stochastic differential equations can be found by solving the Hamilton-Jacobi-Bellman (HJB) equations. It was recently shown that if the optimal control problem has a unique solution, then the desired value function is the adjoint state of a PDE constrained optimization problem, which can be obtained by solving a backward Kolmogorov equation. In direct numerical simulations of incompressible turbulence, driven by a small set of spatial Fourier modes, driver efficiency, turbulent energy content, and dissipation rate will be controlled; uncertainties are accounted for by a noise term.

Objective: We will treat this problem directly, using sparse representations in the spectral ansatz functions combined with via appropriate finite dimensional basis of Hermite polynomials as spectral ansatz functions, where for the high-dimensional problems we will apply low rank tensor product approximation. Particular challenges are the preconditioning of the high-dimensional backward Kolmogorov equation and the treatment of the dominating non-symmetric drift term.